牟合方蓋體積

-
空間中兩半徑為 $r$ 的圓柱垂直相交所形成的立體區域之體積 $V$ 為
$$V=\frac{16}{3}r^3$$


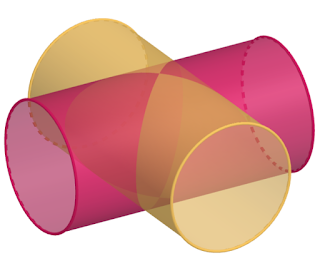
空間中兩半徑為 $r$ 的圓柱垂直相交情況如下圖a

圖(a)



則所交會的區域之立體圖形如下圖b


圖(b)Jason B.


將此圖形中心定為原點架空間座標；因為此圖形八個卦象彼此對稱，所以我們研究其中一卦象即可，其中一卦象之圖形如下圖(c)
圖(c)

則所求即為上圖(c)紅色平面處對 $z$ 軸的面積分
$$V=8 \times \int_{0}^{r}r^{2}-z^{2}  dz=\frac{16}{3}r^3$$


另外此立體曲面之表面積為$A=16r^2$
此立體曲面之英文名稱為Steinmetz solid 


千萬不要只記公式，以下例題就是類似的問題，但不能直接套公式
例題：(106高雄女中)
有一個正方形舞台，邊長為10公分，在四個頂點上架設兩個以對角線為直徑的半圓，交點在舞台中心點的正上方。將鐵絲網佈滿後形成一個鳥籠，請計算出此鳥籠的體積為何？


本文部分圖片取自 https://mathematica.stackexchange.com/  討論串



留言

張貼留言

這個網誌中的熱門文章

向量與面積比

-
圖片
$P$為$\triangle ABC$內一點，且$a\triangle APB$： $a\triangle APC$：$a\triangle BPC=m$：$n$：$k$，則有 $$\overrightarrow{OP}=\frac{k}{m+n+k}\overrightarrow{OA}+\frac{n}{m+n+k}\overrightarrow{OB}+\frac{m}{m+n+k}\overrightarrow{OC}$$ 如圖延長$\overline{AP}$交$\overline{BC}$於$E$點 $case1$：因為$a\triangle APB$：$a\triangle APC=m:n$，所以可得 $\overline{BE}$：$\overline{EC}=m$：$n$，再由分點公式得 $$\overrightarrow{OE}=\frac{n}{m+n}\overrightarrow{OB}+\frac{m}{m+n}\overrightarrow{OC}$$ $case2$：$\overline{AP}$：$\overline{PE}=m+n$：$k$，同樣 由分點公式得 $$\overrightarrow{OP}=\frac{k}{(m+n)+k}\overrightarrow{OA}+\frac{m+n}{(m+n)+k}\overrightarrow{OE}$$ 綜上再將$case1$結果代入$case2$可得 $$\overrightarrow{OP}=\frac{k}{(m+n)+k}\overrightarrow{OA}+\frac{m+n}{(m+n)+k}\times(\frac{n}{m+n}\overrightarrow{OB}+\frac{m}{m+n}\overrightarrow{OC})$$ 經乘開整理可得 $$\overrightarrow{OP}=\frac{k}{m+n+k}\overrightarrow{OA}+\frac{n}{m+n+k}\overrightarrow{OB}+\frac{m}{m+n+k}\overrightarrow{OC...
閱讀完整內容

一路領先問題

-
圖片
不記名投票之下，甲得$m$票，乙得$n$票，且$m\geq n$，開票過程中甲的得票數一路領先乙的得票數之情況總共有 1.當領先狀況允許等於時(甲的得票數 $\geq$ 乙的得票數)$$C^{m+n}_{m}-C^{m+n}_{m+1}$$ 2.當領先狀況不能等於時(甲的得票數 $>$ 乙的得票數)$$C^{m+n-1}_{m-1}-C^{m+n-1}_{m+1-1}$$ 可將原問題轉換為走捷徑問題，舉例來說明： $問$：當甲得$5$票，乙得$3$票時，開票過程中甲的得票數大於等於乙的得票數之情況為何？ 視為下圖 (a)， A走到$Z$的捷徑問題，共有5橫線段3縱線段構成，甲每得一票代表走一小段橫線，乙每得一票代表走一小段縱線，每一個捷徑走法對應到一種得票過程。 圖(a) 如圖(b)，則不難發現線段$\overline{AV}$上的點$A$、$H$、$O$、$V$為得票數平手的局面，例如$O$點即為兩橫兩縱，代表過程中甲得兩票乙得兩票的情況，而這在這個例題中是可以被允許的(得票數大於等於)。且更可以發現綠色的點就是違規的情況，故開票的過程中要避免經過綠色的點。 圖(b) 換句話說，可以先算所有捷徑的走法減去會通過綠色點的走法，即為所求。而要如何算出通過綠色的路徑數量呢？ 首先經過綠色的極限情況是發生在線段$\overline{GU}$上，線段$\overline{GU}$仿佛形成一道界線，故我們從$\overline{GU}$畫一條對稱軸，如圖(c)，並對$A$、$B$、$C$...等三點做對稱於$\overline{GU}$的對稱點$A_1$、$B_1$、$C_1$...這邊只取這三個對稱點當代表，則所有A走到$Z$的捷徑情況都可以被一一對應到從$A_1$走到$Z$的情況，但從$A_1$走到$Z$的所有情況都會經過$\overline{GU}$(及違規)。 圖(c) $C^{8}_{5}$如圖(d)，原始所有路徑(包含違規與不違規) 圖(d) $C^{8}_{6}$如圖(e)，必通過綠色違規路徑 圖(e) 故所求即為$C^{8}_{5}-C^{8}_{6}$ 所以如果題目改成不能等於，則紅色線段$\overli...
閱讀完整內容